Visualizing how to unlearn phrases with negative learning rates

Use negative learning rates to train a language model away from certain phrases! See the progress!

Current state-of-the-art language models have been described as few-shot unsupervised multitask learners. If we have a corpus of text, and explicitly avoid certain phrases, the language model can easily infer the phrases that we tried to excise from our training corpus if it is as effective at analogizing as advertised.

We can use different learning rates, and especially negative learning rates, to penalize our model on these phrases. A small dataset, of integers written out in English, makes it easy to visualize the probabilities over time for various tokens, and see any problems that arise, by visually inspecting the color of a column of pixels that corresponds to the probability for our phrase.

We are trying to get just the last column in the central grey blob to white:

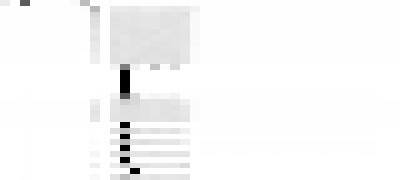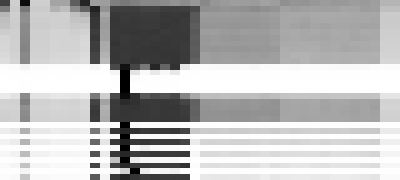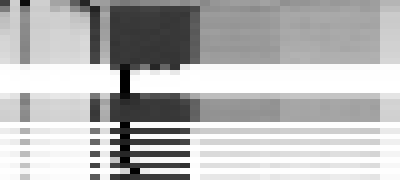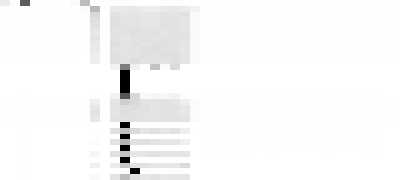
while keeping that corresponding last column grey in the image below:

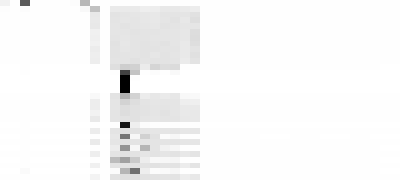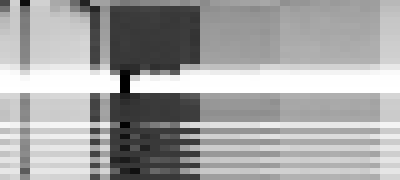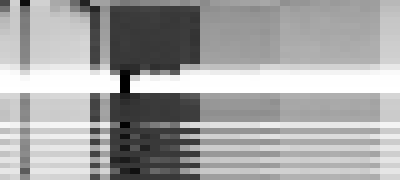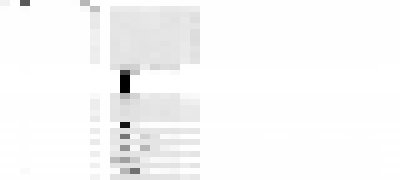
The setup

To consider the problem of training a language model to avoid certain problematic phrases and problematic concepts, consider the problem of training a language model on English readings of integers and training it to avoid any integer that has a 9 digit immediately following a 6: “sixteen thousand nine hundred thirty two” (16932), “six hundred ninety one” (691), and so forth.

We can use an off-the-shelf AWD-LSTM, pretrained on WikiText-103, and train a final layer on the integers from 0 to 100,000 written out. As two gauges of progress in the model, we can monitor what it predicts after the word sixty and after the word fifty: we will be training it with positive examples that include thousand and one through eight, for sixty, while we will be training it with positive examples that include thousand and one through nine for fifty.

Results

Because we have so few different words in our training dataset (40 tokens, specifically), we can visualize the probabilities of what token comes after sixty and fifty as greyscale brightness, where darkness is higher probability, and visually inspect the brightness of a column of interest. We can record the probabilities of each of our forty tokens after each training epoch in the horizontal direction, stack them one after the other in the vertical direction, and jiggle the gamma correction in an animation to highlight differences between low-probability tokens and very-low-probability tokens (any token with lower than 1/256 probability would get blown out to white with no gamma correction). This ends up looking like the following two images, as from above:

sixty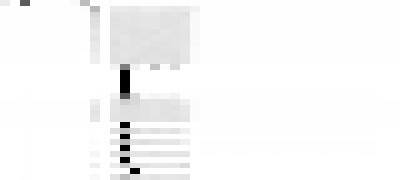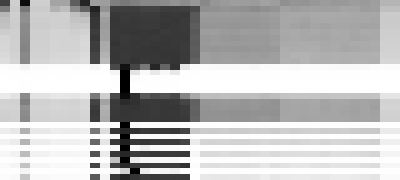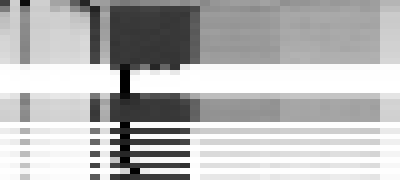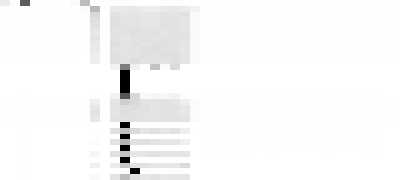

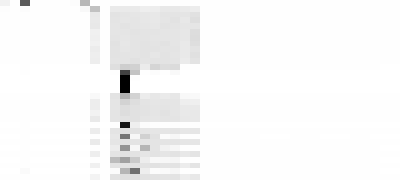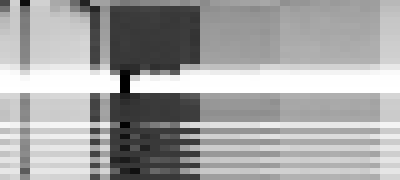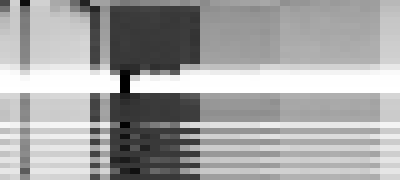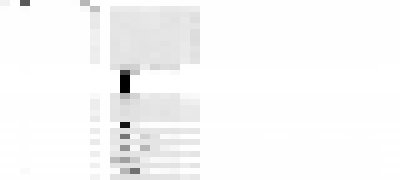
fifty

The top row is where the model starts, highly favoring the “beginning of stream” character, and mostly a wash everywhere else, as an untrained model.

The next ten rows are the next ten epochs, one-cycle learning with a standard positive learning rate, on the corpus which does not any of our forbidden numbers. The bos character is common (implying it would simply generate “sixty”, with no other tokens after), as the stripe on the far left. The large block in the middle is thousand, hundred, and one to nine. Note that “sixty hundred” is very low probability, and is the light stripe between the “sixty thousand” and the “sixty one”/“sixty two”/etc. The last column is nine, and would make a forbidden number after sixty, and it does not appear in our positive training set, although we have see “fifty nine”, and “sixty two”, so our few-shot unsupervised learner of a language model infers it, albeit less commonly than the other digits from one to eight, which is why it appears as a light stripe on the side of that block. Note that in the corresponding image for predicting the word after fifty, in the same column, is not a light stripe for avoiding predicting “fifty nine”.

The next five rows are unlearning, learning at a negative rate, and this is a disaster.

We see, after five epochs of unlearning, that our model collapses, and only predicts two after sixty, and only two after fifty, to the exclusion of all other tokens. That is the vivid black column, indicating how we have mangled our predictions on a larger scale than just for sixty.

After these five epochs are finished, we go back to positive rate learning, with five more epochs of one-cycle learning. Note that after the first epoch of this second round of positive rate learning, the model still overwhelmingly picks two, and only on the next epoch returns to a spread from one to eight, and also welcoming back nine into the probability distribution, which we do not want.

When we alternate negative rate learning and positive rate learning, we avoid this collapse on the positive rate learning. The model after negative rate learning has the same collapse as before, but if we alternate positive rate learning, we can fill out the one to eight block in the middle, and keep the nine column at less probability than the twenty column to its immediate right: our model has seen neither “sixty twenty” nor “sixty nine”, but it thinks “sixty twenty” is much more plausible.

The two lighter blocks to the right are twenty to ninety, and eleven to nineteen. In the initial positive learning rate training, at the top, these are very low probability, but they are even lower at the end, after we stop predicting the word nine after sixty. Further work is needed to widely replicate this in many other scenarios, and to explore how to balance cautiousness around undesirable concepts with explorativeness around unseen concepts, especially when scaling up models beyond toy datasets.

We have made the code to replicate this available online in a notebook.

Conclusions, and further directions

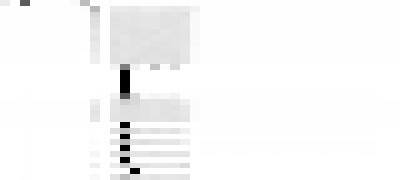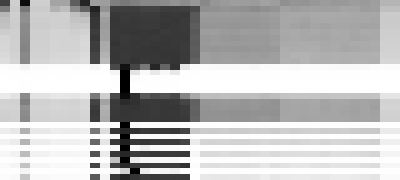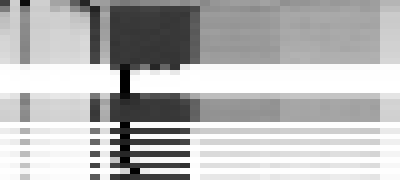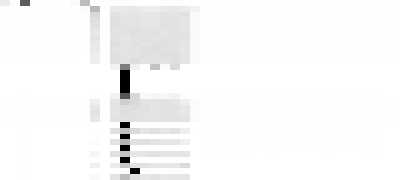
This highly-constrained problem demonstrates steering a language model away from certain words and phrases, and visually confirming the result.

Our success criteria are unusually clear, and our vocabulary is unusually small, so it is possible to spot check the results of training with visual inspection.

This visualization ability, to see when our negative learning rate training causes our language model probability distribution to collapse, is valuable, and we can easily visually confirm when we have fixed the problem.

One urgent next step is to train a much larger language model, on more varied language, with less clear success criteria.

Notably, we can scrub certain concepts and phrases from our training corpus, and it can generalize and extrapolate what we have tried to scrub away.

As we ask larger language models, trained on larger text corpora, to perform larger numbers of tasks, with larger ambiguity about the criteria for success, we can expect larger numbers of unpleasant surprises.

This work attempts to motivate a different direction: we demonstrate that is it possible to explicitly train a language model away from undesirable language, instead of sheltering it from that language, and that only explicit training is effective to decrease its probability of that language, and this explicit training can avoid impacting its probability of other language.

Parallels abound, in casual educational settings and formal educational settings. We have the idea of a cautionary tale, we have the idea of explicit critique to narrate a history and position it as a cautionary tale, we have the idea of structuring this explicit critique in a way that will be easily consumed (delivering positive critique in a group but negative critique in isolation, delivering negative critique as a positive-negative-positive sandwich).

As we bring the people back in to the curation of datasets, we can be more explicit about our training. Instead of training on general “WebText”, we can train towards specific authors we like and away from specific authors we dislike, towards specific texts we like and away from specific authors we dislike, towards specific genres we like and away from specific genres we dislike. This is no substitute for human oversight of the output of the model, and no substitute for human accountability for the output of the model, but is one strategy in the project to be more intentional about how we train our models on specific data with specific biases.